Why Nine Players on Each Team?
One day, three guys were lounging around ye olde tavern with nothing
to do, so they decided to invent baseball. Let’s call
them Abner Doubleday, Alexander Cartwright, and Henry Chadwick because
those were, in fact, their names.
They dithered about how many players would be in each team’s
lineup. Finally, Abner said, “I have a way to resolve
this. We’ll take a random number, say, my birth date (6/26/1819)
without the slashes and parentheses. Then we’ll scramble
the digits good and proper to make a second random number (e.g.,
8619261) and subtract the smaller from the larger. Like 8619261
minus 6261819 equals 2357442. Am I going too fast?”
Alexander grunted and Henry groaned. “Good,” Abner
said. “Now let’s sum the digits in that number:
2 + 3 + 5 + 7 + 4 + 4 + 2 = 27. Next, we’ll sum those
two digits: 2 + 7 = 9. So that’s how many players we’ll
have on each team.”
“Okay,” Alexander yipped. “Now, I’ll
figure out how many innings we’ll play. But I’m
going to use my birth date instead. I was born on April 17,
1820. I’ll shuffle that 4171820 to give me 2011874. So
4171820 minus 2011874 gives me 2159946. I add those digits
to get 36 and add those to get 9. Wow, we’re going to
play nine innings.”
Henry scowled. “Wait a minute. I don’t trust
you hornswogglers. Let me calculate using my birth date—October
5, 1824.” He whipped up a jumbled version of 1051824
and hammered out the math.
“Holy mongoose, Hank!” Alexander shouted. “You
came up with 9, too. That cinches it. Nine it will be.”
We are fortunate that they stumbled onto nine as the number of players
on a team because that is actually the correct number. To demonstrate
this, we’ll use the precise total number of players who have
played in the majors and the Negro Leagues since that
fateful tavern rendezvous: 19,623. We’ll yank out the
comma and rearrange that number (randomly, of course) to get 62193. Now
we’ll
subtract: 62193 minus 19623 equals 42570. Summing these digits
gives us 4 + 2 + 5 + 7 + 0 = 18, and 1 + 8 = 9. QED.
The Pitch that Never Got There
Once there was a pitcher who liked to play around
with numbers. We’ll call him Archimedes
(Arky, for short). Arky figured his figuring
might lead to some new bafflements to torment batters. He
hoped to do a number on them.
One day, Arky’s cunning pitching coach Zeno
said to him, “Arky, you might consider trying
to pitch your curveball so the trajectory velocity
is exactly equal to the spin velocity. I think
you might be surprised by the outcome.”
Arky was flushed with enthusiasm. “I wonder
how many revolutions per minute the ball would have
to make if I threw the pitch with a forward velocity
of, say, sixty miles per hour.” He broke
out the new slide rule his girlfriend Hypatia had given
him for his birthday and calculated thusly: “The
legal circumference of the ball is between 9 and 9.25
inches. If we take the midpoint of that range,
9.125 inches, and . . . [mumble, mumble] . . .” He
also grumbled because the device’s central slider
kept sticking—you always find bugs when you break
in new hardware.
Eventually, he came up with the answer: the pitch
would have to spin at 6,943 revolutions per minute
to have a spin velocity of 60 mph. He frowned
for that is an impossibly high angular rate (curveballs
generally spin in the neighborhood of 2,000 rpm). But
his innate pluckiness carried him right past that moment
of doubt. The ugly frown segued into a high-spirited
grin, and he began working on his new pitch immediately. Before
long, he was ready for the heat of battle.
Confident his clever curveball could not be smacked
or smudged, Arky hurled it as the first pitch to the
first batter he faced. Then a strange thing happened. Immediately
after releasing the ball, Arky said to himself, “I
threw that curveball with a forward velocity of 60
mph and a spin rate of 6,943 rpm. Therefore,
each point on the equator of the ball is traveling
at 60 miles per hour toward the catcher and traveling
at 60 mph around the circumference of the ball. In
this diagram that I am ingeniously drawing in my head
and labeling figure A.1, I can see that as each point
on the ball’s equatorial surface passes position
A, the point will be stationary for an instant [relative
to the catcher]. This is because the point will
be spinning backward toward the pitcher at the same
rate that it is moving forward toward the catcher.”
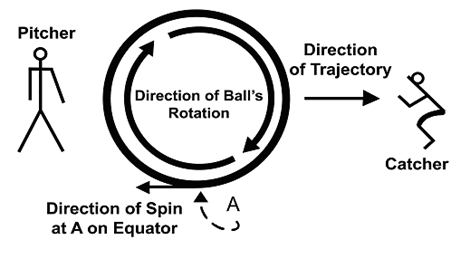
Figure A.1 Diagram of pitch traveling 60 mph toward
the right and spinning with a topspin of 6,943 rpm.
At any instant, some point on the ball’s equator
will be stationary. If one point is stationary,
the rest of the ball (being firmly attached to that
point) must be stationary as well. Thus, the
pitch couldn’t possibly proceed toward the catcher.
The batter waited patiently in the batter’s
box for a while, doing batter-type things like scratching
and amusing himself with a simplified version of tic-tac-toe. But
eventually, he grew weary and gloom-ridden; assuming
the worst, he trudged dejectedly back to the dugout
like an old sack of potatoes.
NOTE: The ball’s shenanigans in our little tale
is ridiculous, of course. But now for a little
known fact—from the viewpoint of a stationary
observer (say, a fan sitting in the bleachers), the
top of the ball moves faster than the bottom on an
overhand curveball with a topspin, just as the top
of a bicycle wheel (with topspin) moves faster than
the bottom of the wheel. And the opposite is
true of an overhand fastball with backspin. This
is explained in terms of cycloid geometry by Martin
Gardner on page 141 of his book aha! Gotcha, published
by W.H. Freeman & Co., 1982.
How Sweet Toes Surprised the Experts
Once upon a time, there were identical twin brothers—Sweet
Toes and Storkhips McGoogel—who wanted to become
baseball players in the worst way. They misspent
their youths taking batting practice three times daily
and became outstanding hitters.
They were such good hitters that they signed lucrative
contracts and worked their way up to the majors. Unfortunately,
both were total klutzes and wanted to practice fielding
about like an ostrich wants to play the kazoo. Thus,
they could man no other position than first base. Fortunately,
they swung the bat so well managers were eager to find
a spot for them on their lineup cards. Each was
forgiven for playing first base like the other.
Strangely enough, year after year, Storkhips had the
highest batting average in the league, and Sweet Toes
always finished second. This, in spite of being
identical in every other aspect. Each season, Storkhips
took home a batting crown, and Sweet Toes went home crownless
and disheartened.
Storkhips and Sweet Toes began their major league careers
on the same day, and they retired ten years later (on
the same day). Except for some difficult spells
of epiplosarcomphalocele (not an easy spell for anyone)
and a few bouts with pig’s feet, Storkhips and
Sweet Toes were steady day-in-day-out performers.
Here are the stats for their ten seasons in the majors
(where AB = at bats, H = hits, and BA = batting average):
Sweet Toes’s Stats Storkhips’s
Stats
Season AB H BA Season AB H BA
1 500 165 .330 1 556 184 .331
*
2 600 204 .340 2 680 232 .341
*
3 610 231 .379 3 510 194 .380
*
4 500 162 .324 4 640 208 .325
*
5 510 167 .327 5 610 202 .331
*
6 600 237 .395 6 500 199 .398
*
7 520 175 .337 7 590 200 .339
*
8 600 233 .388 8 500 195 .390
*
9 600 209 .348 9 620 217 .350
*
10 525 178 .339 10 625 213 .341
*
* Led league
The day they announced their retirements, Storkhips
was given a tour of the baseball Hall of Fame and given
his choice of profiles to be used on his upcoming bronze
plaque (he chose one of Cary Grant’s). And
poor Sweet Toes slouched unnoticed back to Bethlehem,
Pennsylvania, to his thirty-four-room mansion.
But the end of careers means it’s time for the
stats guys to sum things up. When they did, this
is what they got:
Sweet Toes’s Career Storkhips’s
Career
AB H BA AB H BA
5565 1961 .352 5831 2044 .351
Sweet Toes was elated when he saw this. He was
clearly the better batter, so he was awarded the Lifetime
Achievement Award at an elaborate ceremony in North Palm
Springs. He was so uplifted he even decided to
manage the Mets.
Meanwhile, Storkhips was crestfallen. Dejected,
disheveled, and forlorn, he started hanging out with
disgraced politicians and CEOs on the backstreets of
Hollywood. Nobody has seen him since.
Epilogue: This is an example of a phenomenon first described
by statistician G. U. Yule in 1905. It is sometimes
called “Simpson’s paradox,” but it
isn’t really a paradox, and Harry “Suitcase” Simpson
would have nothing to do with it.
Not to Mention India
Willie Theodore was a great hitter in his day—maybe
the best. For good reason, then, he formulated
this clever hypothesis:
1) All
pitchers are stupid.
Now, if that’s true, it follows that:
2) Anyone
who is not stupid is not a pitcher.
And
3) If
2 is true, 1 must also be true.
Eventually Willie reached his middle years and became
a big league manager. Sportswriters and casters
clustered around him daily to collect his extreme quotables,
and this gave him the opportunity to expound his hypothesis
to a wide, gullible audience.
One day, a maverick sportswriter, named Madison, pumped
up his courage to ask Willie, “What evidence do
you have that all pitchers are stupid?” Willie
semi-melted Madison with his steely-eyeball stare for
a minute, and then replied, “You want evidence? I’ll
give you bleeping evidence! First, Dimwitz Smoketosser,
our star pitcher, is stupid. No doubt about that.” All
the media mavens nodded earnestly. Dimwitz had
demonstrated his complete lack of noggin filling on many
occasions.
“Therefore,” Willie continued, “Dimwitz
is evidence supporting the hypothesis that all pitchers
are stupid.” Heads nodded again. All
sportswriters could understand that.
By now, the scribblers were on the edges of their seats,
dropping their pens, fumbling with microphones, sweating
uncontrollably. Willie paused for a wholesome dramatic
effect—then he said, “I happen to know Dr.
Myelin Brainsnapper, a leading college professor at a
leading Midwestern university. He isn’t
stupid at all and he isn’t a pitcher. Therefore,
he is evidence supporting the hypothesis that anyone
who is not stupid is not a pitcher. But since the
truth of this hypothesis implies that ‘All pitchers
are stupid’ is true, well…there you are,
then.”
The journalists looked back at Willie blankly, indicating
that there they weren’t, then. Willie decided
to fill in a little more of the picture for them. “Look,
each one of you is not stupid, and how many pitchers
do we have in the room?”
Not a hand went up. “See? Right there
is a lot more evidence that all pitchers are stupid. We
have a couple of dozen not stupid people here and not
a single one of them is a pitcher.”
A few light bulbs were beginning to flicker over the
heads of the writers, so Willie decided to go for the
big one. “Okay, China has well over a billion
not stupid people and they don’t have a pitcher
amongst them. How’s that for a whole subcontinent
full of overwhelming evidence?”
How much evidence does it take to be overwhelming? Madison
thought for a moment. Then his lips curled into
a demonic grin and an unearthly red glow emanated from
his serpentine eyes. And he took his first step
in his Diogenes-like quest to prove Willie wrong—his
great search for even one pitcher who is not stupid. He’s
still searching.
NOTE: This is a version of Carl Hempel’s raven
paradox, which has been analyzed to near death by logicians. This
little tale should finish it off.

